Categories

Home>Solution> How does a SAM™ work ?

How does a SAM™ work ?

 

How does a SAM™ work ?
    Contents
 
>  1. Aim of SAM
 

Passive mode-locking techniques for the generation of ultra-short pulse trains are preferred over active techniques due to the ease of incorporation of passive devices into various laser cavities.

A passive mode-locking device, the saturable absorber mirror (SAM), can be used to mode-lock a wide range of laser cavities. Pulses result from the phase-locking (via the loss mechanism of the saturable absorber) of the multiple lasing modes supported in continuous-wave laser operation.
The absorber becomes saturated at high intensities, thus allowing the majority of the cavity energy to pass through the absorber to the mirror, where it is reflected back into the laser cavity. At low intensities, the absorber is not saturated, and absorbs all incident energy, effectively removing it from the laser cavity resulting of suppression of possible Q-switched mode-locking. Moreover, due to the absorption of the pulse front side the pulse width is slightly decreased during reflection.
 
>  2. Parameters  
 

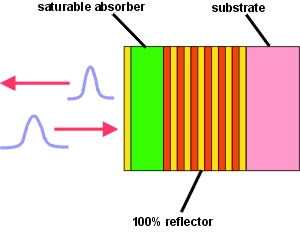
A SAM consists of a Bragg-mirror on a semiconductor wafer like GaAs, covered by an absorber layer and a more or less sophisticated top film system, determining the absorption.
Although semiconductor saturable absorber mirrors have been employed for mode-locking in a wide variety of laser cavities, the SAM has to be designed for each specific application. The differing loss, gain spectrum, internal cavity power, etc, of each laser necessitates slightly different absorber characteristics.

The most important parameters of a SAM are: 		 
 
>  3. Absorption  
  A SAM is a nonlinear optical device. Therefore the absorption A1 depends on the pulse fluence F. If the pulse duration τp is shorter than the relaxation time τ of the absorber material, then the fluence dependent absorption is given by  
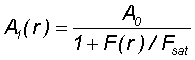  Formula absorption with 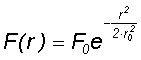Formula fluence eq. (1)  
  A0 small signal saturable absorption  
  F(r) radial dependent fluence of a Gaussian pulse  
  Fsat saturation fluence of the absorber material  
  F0 average value of the pulse fluence  
  r radius, distance from the beam axis  
  r0 Gaussian beam radius  
 
  The effective absorption A of a Gaussian beam is the result of an averaging over the radial dependent fluence F(r) of the pulse:  
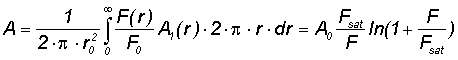  Formula absorption averaging eq. (2)  
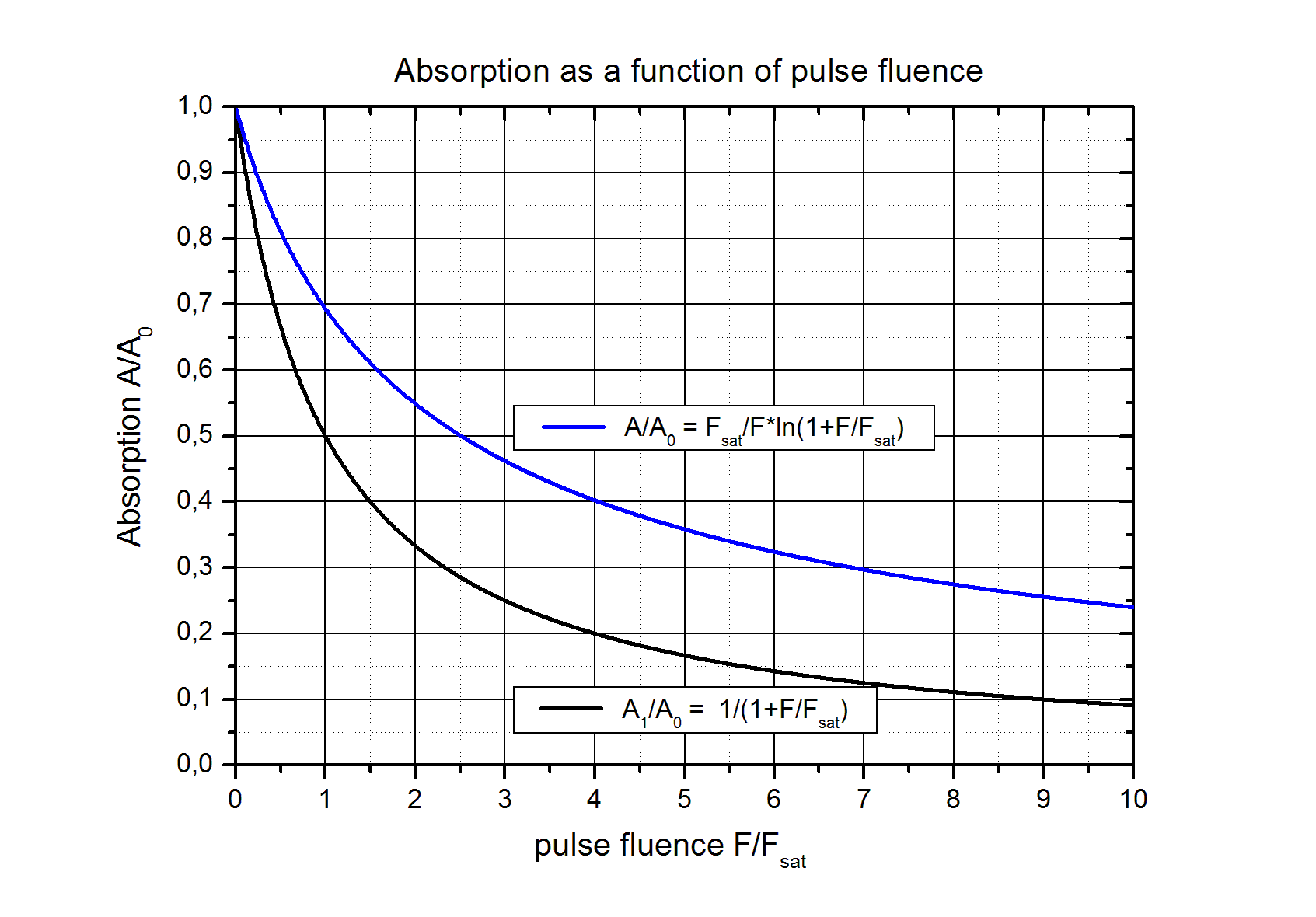
  In the figure below the saturation of the absorption according to equations (1) and (2) (blue curve) is shown. For small fluence F < Fsat the absorption drops down linear with increasing fluence  
 
 
  absorption as a function of fluence  
 
 
 

The small signal absorption A0 is proportional to the square of the electric field strength of the standing wave at the position of the absorber layer. Therefore the saturable absorption of the SAM can be adjusted by the design. A typical value for the saturation fluence Fsat is 50 µJ/cm2.

  
 
  For short pulses the two-photon absorption ATPA increases the total absorption as follows:  
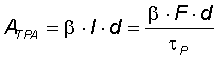  Formula two-photon absorption eq. (3)  
  with β two-photon absorption coefficient  
  I pulse intensity  
  d thickness of the absorber layer  
  F pulse fluence  
  τP pulse duration  
 
 
>  4. Modulation depth ΔR  
 

The reflectance R of a saturable absorber mirror (SAM) is in the region of the stop-band with zero transmittance determined by the absorption A according to R = 1-A. The modulation depth ΔR is smaller than the absorption A0 because of non-saturable losses Ans: ΔR = A0 -Ans. The main reason for the non-saturable losses are crystal defects, which are needed for fast relaxation of the excited carriers. The modulation depth increases with increasing relaxation time t.

Typical values for ΔR are
  • fast absorber with t ~ 500 fs: ΔR ~ 0.5 A0; Ans ~ 0.5 A0
  • slow absorber with t ~ 30 ps: ΔR ~ 0.8 A0; Ans ~ 0.2 A0

The pulse fluence dependent reflection R(F) of a saturable absorber mirror is governed by the effective absorption according to eq.(2). For short pulses and high pulse intensities I the two photon absorption decreases the reflection and therefore also the effective modulation depth according to eq.(3). Therefore the reflectance R of a SAM can be written as

  
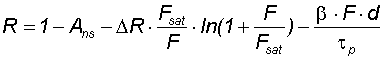  Formula modulation depth eq. (4)  
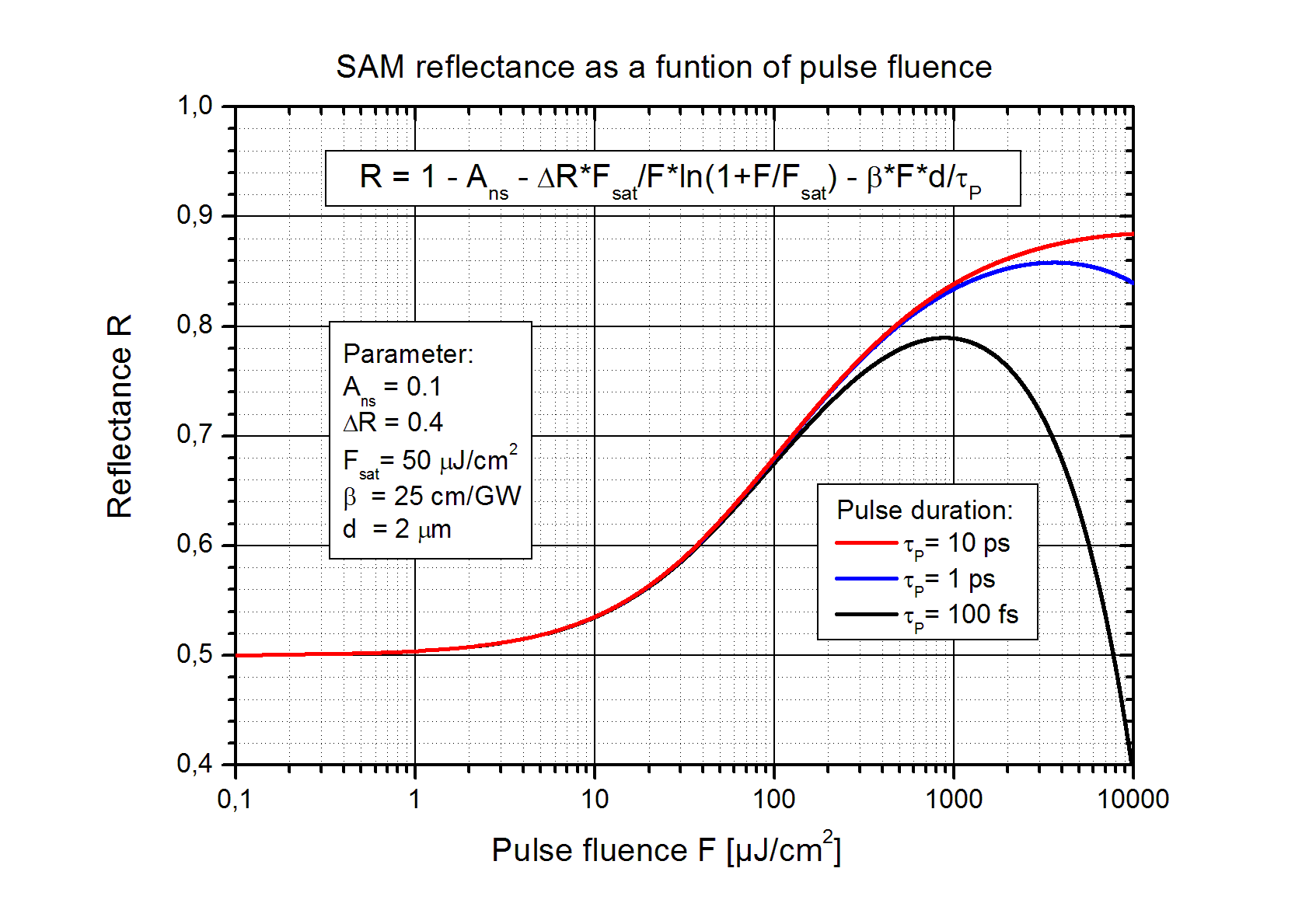
  The calculated SAM reflectance R as a function of pulse fluence F according to eq. (4) is shown for three different pulse durations in the figure below.  
  reflectance as a function of fluence  
 
 
>  5. Relaxation time  
 

The saturable absorber layer consists of a semiconductor material with a direct band gap slightly lower than the photon energy. During the absorption electron-hole pairs are created in the film. The relaxation time t of the carriers has to be a little bit longer than the pulse duration. In this case the back side of the pulse is still free of absorption, but during the whole period between two consecutive pulses the absorber is non saturated and prevents Q-switched mode-locking of the laser.
Because the relaxation time due to the spontaneous photon emission in a direct semiconductor is about 1 ns, some precautions has to be done to shorten it drastically.

Two technologies are used to introduce lattice defects in the absorber layer for fast non-radiative relaxation of the carriers:
  • low-temperature molecular beam epitaxy (LT-MBE)
  • ion implantation.

The parameters to adjust the relaxation time in both technologies are the growth temperature in case of LT-MBE and the ion dose in case of implantation. Typical values of the relaxation time t of SAMs are between 500 fs and 10 ps.

An example of a pump-probe measurement to determine the relaxation time τ is shown below.

  
 
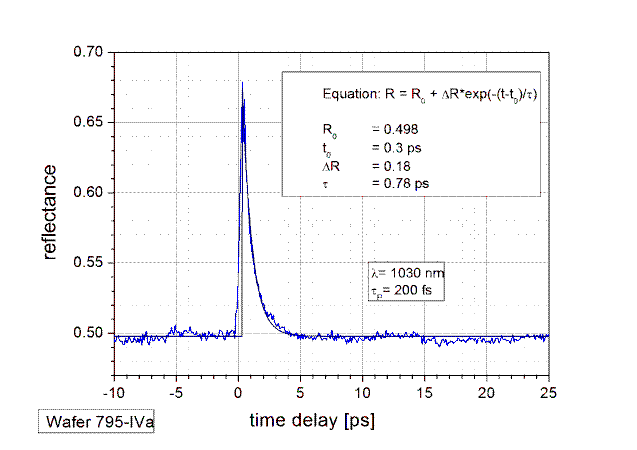  Relaxation time measurement  
 
 
>  6. Saturation fluence Fsat  
 

The saturation fluence depends on the semiconductor material parameters and on the optical design of the SAM. To prevent the SAM from unwanted degradation and destruction due to high pulse fluences, the saturation fluence must be low.
To decrease the saturation fluence, the thickness of the semiconductor absorber layer is reduced below ~ 10 nm. In this case a quantization of the electron energy and the momentum in the direction perpendicular to the absorber layer takes place and as a consequence the density of states decreases below the value of a compact semiconductor. Therefore the absorber layers in a SAM are thin quantum wells with a smaller band gap than the barriers on both sides. If a larger absorption value of the SAM is needed, the number of the quantum wells is increased instead of using a single thick absorber layer.
The electric field intensity in front of the Bragg mirror of a SAM is a periodic function with nodes and antinodes. The absorbing quantum wells are positioned in the antinodes to get a low saturation fluence. Together with the Fresnel reflectance at the semiconductor-air boundary the Bragg mirror builds a Fabry-Perot like resonator, which contains the quantum wells. The optical thickness of the semiconductor material between the reflectors determines the cavity to be resonant or anti-resonant. The saturation fluence of a resonant SAM is lower than that of an anti-resonant SAM because of the field enhancement inside the cavity.

  
 
 
>  7. Absorber temperature  
 

The saturable absorber converts a part of the incoming photon energy into heat. This thermal energy increases the absorber layer temperature during and shortly after an optical pulse. After that the heat is transported through the substrate to the heat sink on the rear substrate side. In case of a substrate like GaAs with a high thermal conductivity only a negligible amount of the dissipated heat goes trough the front surface of the absorber into air.
In case of a pulsed laser beam the absorber temperature T varies periodically with the pulse repetition rate f. A continuous heat flow from the absorber layer to the heat sink leads to a constant absorber temperature rise ΔTstat.
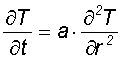The heat diffusion into the GaAs substrate and the resulting temperature distribution T(r,t) can be described by the heat diffusion equation (5)

  
  heat diffusion equation eq. (5)  
 

If the laser spot radius r on the absorber surface is small in comparison to the substrate thickness (typically 0.5 mm) then the heat flow in the absorber layer is nearly one dimensional but in the substrate three dimensional (with a point source). Then the heat is distributed into a half space of the substrate resulting in a temperature field with nearly concentric interfaces of equal temperature.
If we consider at first the time average temperature increase delta Tstat of the absorber layer caused by the mean absorbed optical power Pm, then we can use the following relations for a centre symmetric three dimensional heat flow:

  
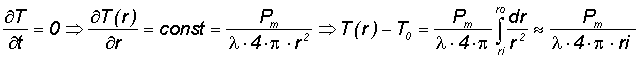  static temperature difference eq. (6)  
 

Here λ is the thermal conductivity, ri is the inner (illuminated) radius of a sphere and ro an outer radius of a sphere with the heat sink temperature T0. The approximation used is ri « ro when we consider the GaAs wafer thickness as ro substantial larger then the laser spot radius ri=r. The mean absorbed optical power is

  
  static temperature difference eq. (7)  
 

To take into account that the heat flow is only into a half space (not to air) and that in the vicinity of the absorber layer the flow is nearly one dimensional (not three dimensional as calculated) the real temperature rise is about by a factor of 4 higher then in the above formula (6), so that

  
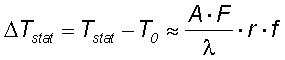  static temperature difference eq. (8)  
 

If the laser spot radius r is larger then the substrate thickness d then the heat flow is nearly one dimensional and then r must be replaced by d in the above equation (8).
The time dependent solution of the one dimensional heat equation within the absorber layer can be estimated using the response of the system on a Dirac delta function, which simulates the heating at z=0 during a short laser pulse. The temperature evaluation near the surface (z2 < 4at) after the laser pulse at t>tp can be written in this case as

  
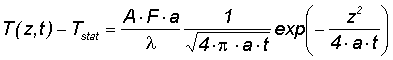  dynamic temperature difference eq. (9)  
 

Here the heated volume after the laser pulse is approximated by the product of the illuminated area and the diffusion length (4at)1/2.
The maximum temperature of the absorber layer at z=0 can be expected after the absorbed optical energy is converted into heat. This is roughly after the sum of the pulse duration tp and the carrier relaxation time τ

  
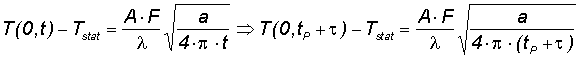  maximum temperature difference eq. (10)  
 

The maximum total absorber temperature increase ΔTmax can be described by the sum of the time dependent dynamical part ΔTdyn(τ+tp) and the static part ΔTstat.

  
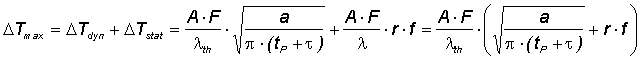  maximum absorber temperature eq. (11)  
  with ΔT temperature rise  
  A absorption  
  F pulse fluence  
  λth thermal conductivity of the absorber material (55 W/(mK) for GaAs)  
  a thermal diffusivity of the absorber material (3.1 10-5 m2/s for GaAs)  
  tp optical pulse duration  
  τ carrier relaxation time in the absorber  
  r spot radius on the absorber  
  f optical pulse repetition rate  
 
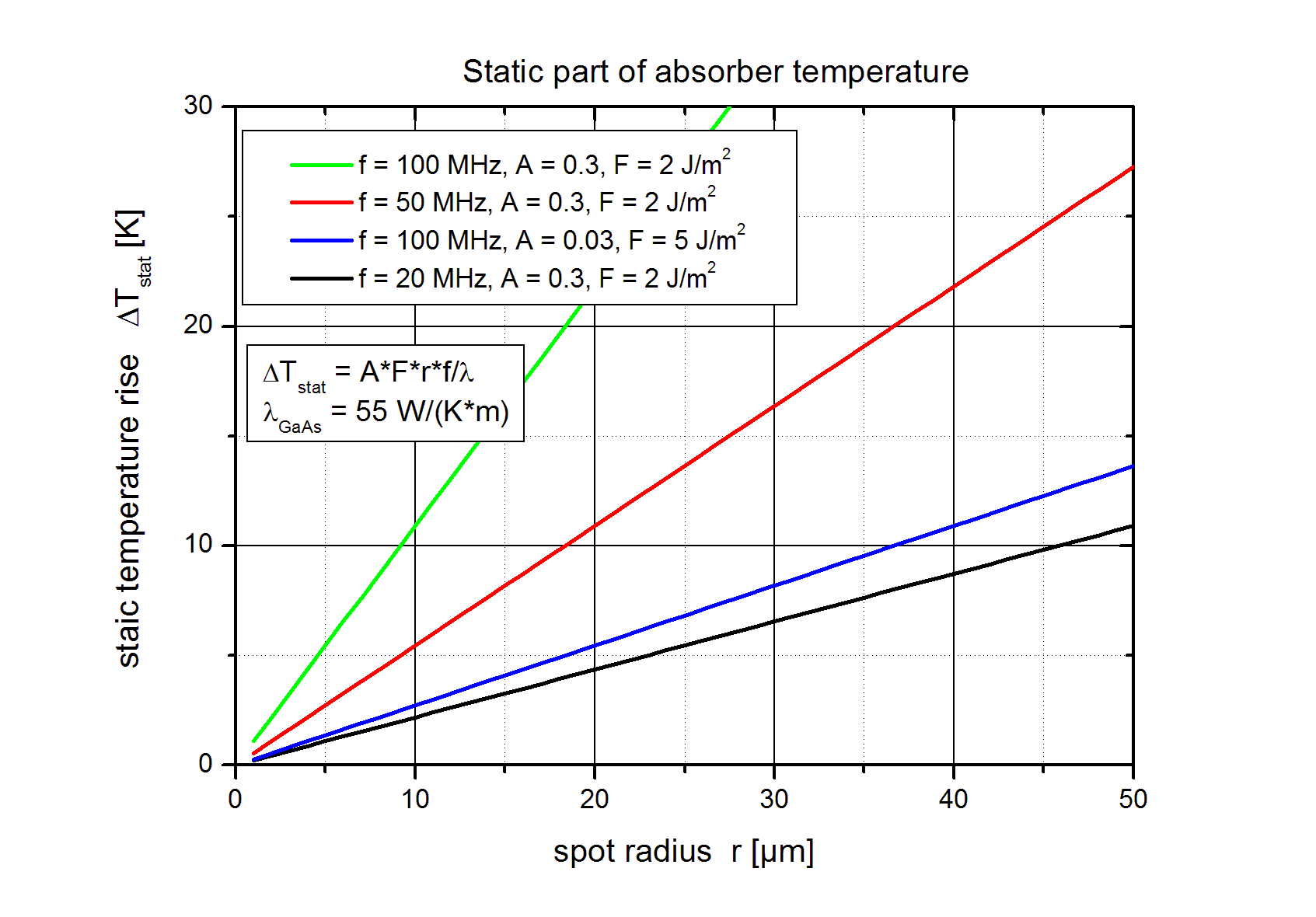
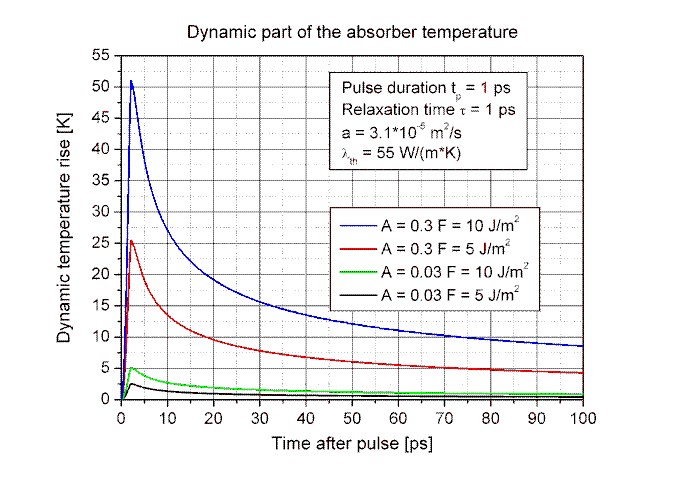
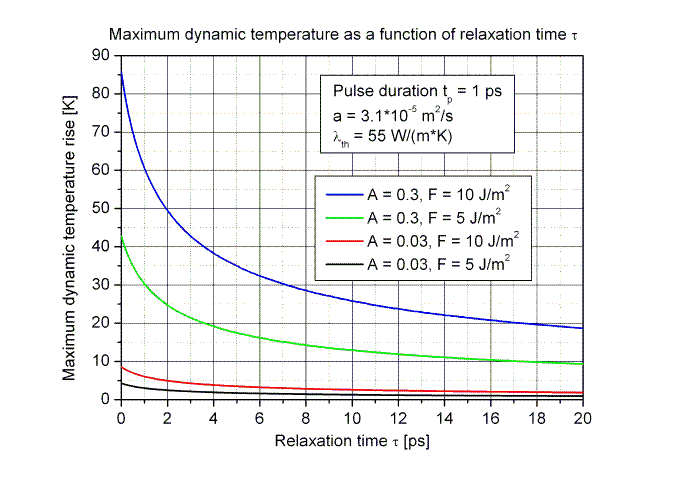
  The two figures below show the static temperature rise ΔTstat as a function of the optical spot radius r and the dynamic temperature rise ΔTdyn as a function of the absorber relaxation time for typical parameters in solid state (absorption A = 0.03) and fiber lasers (absorption A = 0.3) according to eqs. (9) and (11).  
  dynamic temperature rise of the saturable absorber  
  dynamic temperature rise of the saturable absorber  
 
  The maximum temperature rise decreases with increasing absorber relaxation time τ because the absorbed energy is released from the excited electrons into the crystal lattice after the relaxation time. If the relaxation time τ is longer then the pulse duration tp the electrons store the absorbed energy for a short time whereas the thermal energy diffuse already from the absorber layer into the substrate.  
  maximum temperature rise of the saturable absorber  
 
 
>  8. Reflection and absorption bandwidth  
 
  7.1 Time-bandwidth product (TBWP)  
  From Heisenberg's uncertainty principle for the conjugated variables pulse width Δt and photon energy E = hν the TBWP of a laser pulse is limited to about Δt.Δν ≥ 1/(2π).
  • h = 6.626 . 10-34 Js is Planck's constant
  • ν the pulse mean frequency and
  • Δν the pulse bandwidth
An accurate calculation shows, that the minimum TBWP for a Gaussian pulse is Δt.Δν = 0.44 (pulse duration in seconds x pulse bandwidth in Hertz > 0.44).

The minimum TBWP for a Sech2pulse is Δt.Δν = 0.32 .

Most people do not work with frequency ν but prefer wavelength λ. Using the relation c=λ.ν the frequency interval Δν is related to the wavelength interval Δλ by Δν = - c. Δλ/λ2.
c = 2.988 . 108 m/s is the speed of light in the vacuum.		  
 
  Numerical values for the minimum bandwidth Δν as a function of pulse duration Δt  
 
Pulse
duration
Δt		 Gaussian
bandwidth
Δν		 Sech2
bandwidth
Δν		 Gaussian bandwidth Δν
Sech2 bandwidth Δν
5 fs 88 THz 64 THz Bandwidth
10 fs 44 THz 32 THz
20 fs 22.THz 16 THz
50 fs 8.8 THz 6.4 THz
100 fs 4.4 THz 3.2 THz
200 fs 2.2 THz 1.6 THz
500 fs 880 GHz 640 GHz
1 ps 440 GHz 320 GHz
2 ps 220 GHz 160 GHz
5 ps 88 GHz 64 GHz
10 ps 44 GHz 32 GHz
20 ps 22 GHz 16 GHz
down
 
 
  Numerical values for the minimum bandwidth in nm as a function of pulse duration Δt  
 
Pulse
duration
Δt		 Gaussian bandwidth (nm) Sech2 bandwidth (nm)
@ 800 nm @ 1200 nm @ 1600 nm @ 2000 nm @ 800 nm @ 1200 nm @ 1600 nm @ 2000 nm
5 fs 188 nm 424 nm 752 nm 1180 nm 137 nm 308 nm 547 nm 858 nm
10 fs 94 nm 212 nm 377 nm 590 nm 68 nm 154 nm 274 nm 429 nm
20 fs 47 nm 106 nm 188 nm 295 nm 34 nm 77 nm 137 nm 214 nm
50 fs 19 nm 42 nm 75 nm 118 nm 13 nm 31 nm 55 nm 86 nm
100 fs 9.4 nm 21 nm 38 nm 59 nm 6.8 nm 15 nm 27 nm 43 nm
200 fs 4.7 nm 10.6 nm 18.8 nm 29.5 nm 3.4 nm 7.7 nm 13.7 nm 21.4 nm
500 fs 1.9 nm 4.2 nm 7.5 nm 11.8 nm 1.4 nm 3.1 nm 5.5 nm 8.6 nm
1 ps 0.94 nm 2.12 nm 3.77 nm 5.90 nm 0.69 nm 1.54 nm 2.74 nm 4.29 nm
2 ps 0.47 nm 1.06 nm 1.88 nm 2.95 nm 0.34 nm 0.77 nm 1.37 nm 2.14 nm
 
 
 
  7.2 Reflection bandwidth  
 

The reflection bandwidth of the SAM has to be larger than the pulse bandwidth. In case of a SAM with an underlying Bragg-mirror the reflection bandwidth is determined by the ratio of the refractive indices nH/nL of the layers in the thin film stack. More about Bragg-mirrors ...

The relative spectral width w = Dl/l of the high reflectance zone of a conventional semiconductor AlAs/GaAs thin film stack is about 0.1. Therefore the width of the high reflection zone of an AlAs/GaAs Bragg-mirror with a center wavelength of 1000 nm is about 100 nm. From the tables above this results in a minimum pulse duration of about 20 fs. For shorter pulses other mirror types, for instance dielectric or metallic mirrors has to be used.

  
 
 
  7.3 Absorption bandwidth  
 

An ideal SAM has a constant saturable absorption for all wavelengths of the pulse spectrum. Because of the wavelength dependence of the absorption in a semiconductor material above the band gap, the absorption increases with decreasing wavelength. In case of a resonant SAM this dependency may be changed by the standing waves inside the cavity in such a way, that the maximum absorption is at the resonance wavelength of the SAM.